
Climatología
La climatología durante un eclipse total de Sol
Análisis de los datos obtenidos en la colina de Gyugy Hát
Estudio de las variaciones del microclima de la región del lago Balaton (Hungría) durante el eclipse total de sol del 11 de agosto de 1.999
Por Aniceto Porcel Rosales, Antonio Jesús Torres Gil y Cristóbal Marín Molina
INTRODUCCIÓN
El presente estudio está encuadrado dentro del programa llevado a cabo por la expedición TOTAL ´99 organizada por la Sociedad Astronómica Granadina (SAG) para la observación del eclipse total de sol del 11 de agosto de 1.999 en la región del lago Balaton en Hungría.
Durante la preparación de la expedición se consideró muy interesante realizar un estudio climatológico que mostrara cómo afecta un eclipse total de sol a la atmósfera terrestre. La intención era colocar todo el instrumental unos días antes del eclipse y continuar las medidas 1 ó 2 días después. Con ello se pretendía muestrear, con cierto margen, el comportamiento climatológico de la zona, sobre todo a lo largo de la primera mitad del día, y compararlo con el periodo correspondiente a la ocultación del Sol por la Luna. Las circunstancias lo impidieron y sólo se pudo tener operativa toda la estación meteorológica el día del evento. A pesar de esto, los datos obtenidos son muy relevantes y denotan un comportamiento muy dependiente y sincronizado con la evolución del eclipse.

Imagen del Sol eclipsado donde se aprecia la corona solar
Alberto López - SAG/TOTAL '99
El tiempo en la zona del lago Balaton estuvo despejado el 11 de agosto de 1.999. No obstante, su evolución en las jornadas previas provocó momentos de incertidumbre. Sabíamos que la región era propensa al desarrollo de tormentas de convección en la tardes de verano y un ejemplo de esto lo tuvimos a nuestra llegada al lago el 7 de agosto, donde fuimos recibidos con una fuerte tormenta con gran aparato eléctrico. Pese a que los días posteriores no fueron especialmente favorables, el comportamiento del tiempo era esperanzador. El momento crítico se dio la tarde anterior al eclipse, martes 10 de agosto. A partir de las 16 horas comenzó a cubrirse el cielo con un gran manto de nubes denso y oscuro, que hizo presagiar lo peor. Las cadenas de TV europeas informaban de forma continua sobre el tiempo reinante en todas las zonas por donde iba a pasar la sombra, así como las previsiones para el día posterior. Las expectativas apuntaban a que la situación no podía ser peor, pues no existía ningún lugar de Europa, incluida Hungría, donde se pudiese albergar esperanza. Concretamente para dicho país, se anunciaban cielos cubiertos de forma intermitente en la zona montañosa donde estábamos localizados y lluvias en la gran llanura Húngara. Solo cabía esperar y rezar. Así y todo, la situación presentada por los partes meteorológicos mostraba que estábamos situados en el paso de dos frentes nubosos y que entre ambos quizás pudiera darse un hueco a la hora y en el lugar precisos. Esa tarde especulamos que si rompía a llover la atmósfera podría limpiarse y proporcionar el tan deseado cielo despejado. Cuando llegó la noche la lluvia aún no había aparecido, pero el cielo mostraba algunos huecos entre las capas de nubes, lo que permitió ajustar los telescopios a la Polar y seguir esperando. Hacia las 3 UT de la mañana la lluvia llegó en forma de torrente. Todo el instrumental tuvo que ser retirado de forma apresurada. Pese al inconveniente, la situación era la que durante toda la tarde anterior se estuvo esperando. El amanecer apareció casi despejado y esta situación mejoró conforme se iba acercando el eclipse. El lago Balaton fue uno de los pocos lugares de Europa donde se pudo contemplar, sin apenas nubes, cómo la Luna ocultaba a nuestro astro rey. Evidentemente la "suerte" corrió a nuestro favor. Sin embargo, en cierto modo fue una suerte forzada, ya que los datos de estadísticas climatológicas consultados para la elección de la zona, mostraban unos porcentajes más favorables allí que en el resto de Europa central. Aunque estas informaciones preliminares indicaban que las zonas más óptimas eran las que la sombra cubriría en su recorrido asiático.
Los parámetros medidos fueron los siguientes:
-
Temperatura ambiente: al Sol y a la sombra.
-
Presión atmosférica.
-
Humedad relativa.
-
Velocidad del viento.
-
Índice de nubosidad
ALGUNOS DATOS SOBRE EL ECLIPSE
Este eclipse fue el vigésimo primero del ciclo de saros número 145, que se inició el 4 de enero de 1639 y tendrá su final el 17 de abril del 3009, constando de 77 eclipses en casi 14 siglos.
La sombra lunar tuvo una anchura media de 100 Km. y recorrió unos 14.000 Km. a lo largo de la superficie terrestre en poco más de tres horas. Su velocidad media de avance fue de 4.500 Km./h (1,25 Km./s), dando sus valores máximos al principio y al final de su recorrido y los mínimos en la mitad, con un valor de 2.450 Km./h (0,680 Km./s).
Se dio como total en una franja que comenzó en pleno océano Atlántico Norte, al sur de Terranova, y tuvo su primer contacto terrestre en el continente europeo en las islas Scilly, al sur de Inglaterra, a las 10h 10m UT. Más tarde, tras cruzar el Canal de la Mancha, tocó Francia por las costas de Normandía, pasando a unos 30 Km. al norte de París. A continuación atravesó Bélgica, Luxemburgo, Alemania y Austria. A las 10h 46m UT llegó a Hungría, donde la fase total ya superaba los 2m 20s. Más tarde entró en Rumania, donde se dio el máximo del eclipse en la ribera del río Olt, al suroeste de la ciudad de Rimnicu-Vilcea, con una duración de 143s a las 11h 03m 05s UT y con el Sol a una altura sobre el horizonte de 59º. La sombra lunar abandonó a las 11h 13m UT por la costa de Sabda para adentrarse en el Mar Negro y Turquía. Seguidamente cruzó Siria, Irak, Irán y Pakistán. A las 12h 28m UT llegó a la India, donde pocas ciudades disfrutaron de un minuto escaso de totalidad. El último contacto de la sombra con la Tierra se produjo a las 12h 36m 24s UT en el Golfo de Bengala, a unos 600 Km. al sur de Calcuta.
El emplazamiento del campo de observación de meteorología estaba desplazado unos kilómetros al Suroeste de Siofök, en consecuencia los tiempos para los diferentes contactos han de ser adelantados unos 12 segundos respecto de los de la tabla, quedando la fase de totalidad reducida en unos 5 segundos.
Las efemérides del eclipse para la ciudad de Siofök son las siguientes:
CONDICIONES GENERALES DEL MICROCLIMA DE LA REGIÓN DEL LAGO BALATON DURANTE EL VERANO
La información de que disponíamos sobre la región del Lago Balaton (el mayor de centroeuropa) es que es una zona con una climatología estable durante el verano, con periodos de hasta cuatro semanas de situación anticiclónica, con muy bajas concentraciones de vapor de agua atmosférico. Siofök, localidad al borde del lago Balaton, tiene una temperatura media durante el mes de agosto, de 20,9º C, con oscilaciones entre 35º C y 10º C por la noche, y unas precipitaciones medias de 59,2 l/m2. Las tormentas veraniegas no son inusuales en esa zona, pero su máximo desarrollo se da hacia las 6 de la tarde. La nubosidad es escasa a las primeras horas del día y su desarrollo se da habitualmente a las últimas horas de la mañana a escasa altura sobre el horizonte, apareciendo hacia el sur de los montes que rodean el lago.
Nuestra experiencia es que en líneas generales estas condiciones se cumplieron durante los días que pasamos en la zona, aunque con algunos matices. Entre estos cabe destacar que la tasa de concentración de vapor atmosférico fue relativamente alta durante nuestra estancia.
DESCRIPCIÓN DE LA EXPERIENCIA
A la hora de realizar las mediciones atmosféricas se requería un lugar con una cota superior a la media de la región y con horizontes despejados, para facilitar la toma de datos de luminosidad ambiente. Además se buscaba una zona sin obstáculos que dificultasen las medidas de velocidad del viento. En definitiva, un espacio abierto era lo más adecuado para la mayoría de la toma de datos. Se escogió una pequeña colina, en Gyugy Hát, situada a unos 311 m de altura y desde la que se podía divisar una panorámica de la orilla Sur del lago Balaton.
Nuestro instrumental consistía en una estación meteorológica compuesta del siguiente material:

Localización de la estación meteorológica en Gyugy Hát
-
Dos termómetros de alcohol con una precisión de 1º centígrado, uno de los cuales fue utilizado para medidas de temperatura al sol y el otro para medidas de temperatura a la sombra.
-
Un termómetro de máximas y mínimas de mercurio con una precisión de 1º centígrado.
-
Un barómetro aneroide con una precisión de 1 mb.
-
Un higrómetro analógico ESCHENBACH con una precisión del 1%
-
Un anemómetro digital con una precisión de 0.1 m/s, cedido por el servicio meteorológico del aeropuerto de Granada.
La recogida de datos se realizó a partir de las 8:24 UT y se prolongó hasta las 12:54 UT. Debido a la cambiante situación meteorológica en la región durante aquellos días, fue imposible contrastar estos datos con mediciones durante los días previos y posteriores, lo que se ha suplido mediante consultas realizadas a través de Internet acerca de la climatología local.
TEMPERATURA AMBIENTE
La temperatura se tomó tanto a la sombra como al Sol. Como se ve en la gráfica ambas líneas evolucionan de forma similar en el tiempo, pero con una clara tendencia a solaparse en la totalidad. La explicación de este fenómeno es obvia: conforme se aproxima el máximo del eclipse la radiación solar va disminuyendo, haciendo que las diferencias entre ambas temperaturas sea menor y culminando esto en el centro de la totalidad, donde las respectivas medidas se corresponden, por decirlo de alguna forma, con "temperaturas a la sombra", ya que el Sol está ocultado por la Luna. Este comportamiento se invierte al salir de la totalidad.

La temperatura mínima alcanzada fue de 20º C y se da casi simultáneamente con la totalidad. Este hecho merece ser analizado con más detalle. Si tenemos en cuenta un comportamiento inercial cabe esperar que el máximo del eclipse no se sincronice temporalmente con la mínima temperatura, pues esta se dará con cierto retraso en el tiempo. En nuestro caso esto no es así, ya que el valor mínimo se solapa claramente con el inicio de la totalidad. Cabe especular que antes de que el disco solar sea completamente ocultado, la insolación llega a ser tan reducida, que la temperatura desciende significativamente hacia el valor mínimo, independientemente de los valores de luminosidad ambiente.
En cambio a la salida de la totalidad la recuperación se hace con mayor lentitud, tardando unos 11 minutos en elevarse un grado (temp. sol). Es como si las masas de aire tardarán más en reaccionar ante la elevación del flujo de radiación que a la reducción de este.
Si observamos detenidamente la gráfica comprobamos que el descenso de la temperatura comienza a ser significativo a partir de las 10:06 UT. En esta hora el eclipse está aproximadamente en la mitad en su camino hacia la totalidad, lo que indica que, con un 50% del Sol ocultado, el efecto sobre la temperatura ya es claro. En cambio, no se puede deducir una influencia directa del eclipse en la evolución de la temperatura en los minutos anteriores (desde 9:26 UT, hora de comienzo del eclipse, hasta las 10:06 UT).
Por el contrario, el desarrollo posterior a la totalidad se presenta más lineal, dándose una elevación constante de las temperaturas hasta las 12:13 UT (fin del eclipse) y con unos valores máximos de 29º C al Sol y 26º C a la sombra. A partir de este instante las curvas se aplanan con una oscilación mínima.

Antes del eclipse (desde las 8:26 UT hasta las 9:26 UT) las oscilaciones de los valores medidos, sobre todo en las temperaturas al Sol, se deben a la inestabilidad del comienzo de la mañana, donde aún se notan los efectos de la tormenta que se desarrollo durante la noche anterior. Esto se ve en el índice de nubosidad, que a esas horas se muestra más elevado y en continuo cambio. Probablemente sea la causa principal de las variaciones de las temperaturas al Sol. Las valores máximos de este periodo son de 28º C para el Sol y de 24º C para la sombra, mostrando una tendencia al descenso, incluso antes del comienzo del primer contacto.
En líneas generales se puede decir que la evolución de la temperatura durante el eclipse se muestra altamente lineal a partir de la segunda mitad de la primera fase parcial. Las diferencias encontradas entre el comienzo del eclipse y su salida son atribuibles al habitual desarrollo de la temperatura a lo largo de un típico día de verano en la región y a la tormenta de la noche previa.
PRESIÓN ATMOSFÉRICA
La presión atmosférica muestra un comportamiento en el tiempo similar a la temperatura.
Las primeras medidas de la mañana (desde las 8:26 UT hasta las 10:16 UT) arrojan un valor constante de 985 mb. Grosso modo podemos decir que en la primera mitad de la fase de entrada no hay efectos apreciables, en el margen de resolución del instrumental empleado. Hacia las 10:26 UT desciende a 984 mb. Si comparamos esto con los primeros descensos significativos de temperatura comprobamos que la presión reacciona con un retraso de unos 20 minutos. La caída continúa hasta las 10:40 UT, es decir, hasta unos 9 minutos antes del comienzo de la totalidad y se mantiene constante hasta la 10:57 UT.

Queda claro que este elemento reacciona de forma inercial, al mostrar a la salida de la totalidad una evidente lentitud en la recuperación de sus valores. Este comportamiento es diferente al de la temperatura, ya que esta muestra una gran sincronía con el comienzo de la totalidad y, por el contrario, la presión se adelanta en su valor mínimo al comienzo de la fase total. En cambio, frente a los 11 minutos que tarda en reaccionar la temperatura, la presión solo se retrasa unos 8 minutos hasta comenzar su ascenso.
El ascenso de la curva en la fase de salida se caracteriza por periodos de elevación lineal alternados con otros de estancamiento, alcanzando la normalización de sus valores unos 30 minutos antes del fin del eclipse. El máximo de 986 mb alcanzado desde las 12:03 UT hasta las 12:13 UT, se puede considerar valores fuera de la tendencia.

En general, la presión muestra un descenso leve de solo 3 mb lo largo del desarrollo del eclipse y con una ligera diferencia entre la fase de bajada y la de subida, definida por una recuperación ascendente menos uniforme
HUMEDAD RELATIVA
La humedad relativa indica el porcentaje de concentración de vapor de agua en el aire respecto a la concentración cuando el mismo está saturado (100%). En nuestra experiencia, esta sigue unas pautas inversas a los demás elementos analizados, mostrando una tendencia a la elevación durante el periodo del eclipse, con un comportamiento donde no se reflejan de forma nítida las fases del mismo, pero sí claramente dependiente de él. Esta elevación en la concentración del vapor de agua en las capas inferiores de la atmósfera es consecuencia de la bajada de insolación y por tanto, del nivel de saturación del aire.

Durante las primeras horas (desde las 8:26 UT hasta las 9:26 UT) su avance es irregular, con valores que oscilaron entre el 72% y el 76%. Esto esta ligado a diferentes factores como la tormenta de la noche, el índice de nubosidad y la inclinación de los rayos solares sobre la superficie terrestre. Posteriormente se da una estabilización entorno al 70 % hasta las 10:36 UT, momento en que comienza un incremento de los valores que culmina en un 85 % a las 11:03 UT, hora en la que empieza a decrecer.
De forma lógica es de esperar que a lo largo del día haya una reducción de la humedad relativa ligada a la elevación del sol sobre el horizonte y el consiguiente aumento de la radiación. Las posibles oscilaciones de la humedad a su vez pueden estar relacionadas, entre otras causas, a una mayor o menor concentración de nubes. Durante la mañana del 11 de agosto, en el periodo comprendido desde las 8:26 UT hasta las 9:16 UT el Sol se elevó desde los 46,18º hasta los 52,58º sobre el horizonte, con lo cual cabía esperar que la humedad disminuyera. Sin embargo, si observamos el gráfico vemos que la evolución de esta viene marcada por oscilaciones en ambos sentidos, lo que se explica por el desarrollo de la nubosidad. Así tenemos que a las 9:16 UT la humedad aumento hasta un 76% que coincide con un incremento de nubes que cubrían el cielo en un 75% unos minutos antes. A partir de aquí y hasta las 9:46 UT la humedad baja al igual que la nubosidad, con un leve incremento posterior de ambos elementos. Después el índice de nubosidad desciende hasta un 13%, sin embargo la humedad aumenta, a pesar de que el Sol se encuentra a más de 58º sobre el horizonte, lo que demuestra que estos elementos se disocian en su comportamiento y la humedad queda claramente dependiente de la evolución del eclipse.

La elevación de la humedad, que se da hacia las 10:36 UT, se sitúa algo después de la mitad de la primera parcialidad, circunstancia que lo asemeja a la presión aunque de forma inversa y algo retrasada. La totalidad queda encuadrada casi al final de los valores máximos, y al contrario que para los otros elementos, no queda claramente definida en la curva. El comienzo del descenso es coincidente con el de la recuperación de la presión.
La humedad es el elemento que muestra más tendencia a la inercia en su desarrollo quedando, en consecuencia, más enmascarados los puntos de cambio que marcan su evolución respecto del eclipse.
VELOCIDAD DEL VIENTO
La interpretación del comportamiento de la velocidad del viento durante la mañana está caracterizada por significativas oscilaciones, con una tendencia general a la bajada en consonancia con el desarrollo del eclipse.

Es difícil situar el punto que marca claramente el descenso de los valores de este elemento hacia la totalidad, aunque este puede ser situado hacia la 10:08 UT, que es el centro de la primera parcialidad, con una velocidad de 4,5 m/s. Desde este momento hasta el centro del eclipse solo se da un máximo puntual de 2,8 m/s y las oscilaciones medias descienden a valores próximos a 1 m/s. La totalidad comienza con 0,6 m/s y termina con un valor de 0 m/s. Este se extiende unos 7 minutos más tarde con una ligera elevación a 0,5 m/s a las 11:01 UT y una nueva caída a 0 m/s desde las 11:11 UT a las 11:17 UT. A partir de aquí comienza un aumento de la velocidad caracterizado por oscilaciones similares a las que dieron en la bajada, aunque algo más regulares en su evolución temporal.

El valor máximo de este parámetro durante la primera fase del eclipse es de 6,2 m/s, y de 3,8 m/s a la salida, ambos situados en los extremos más opuestos de sus respectivas fases. El mayor valor medido durante la mañana es de 7 m/s aunque este se da ya fuera del eclipse a las 12:40 UT.
ÍNDICE DE NUBOSIDAD
El cálculo del índice de nubosidad se realiza por el método llamado de los octavos. Para ello se procede de la siguiente forma:
Se divide mentalmente la bóveda celeste en ocho parte iguales según el siguiente esquema

Según la extensión de la nubosidad adjudicamos una fracción correspondiente a la porción o porciones cubiertas. Por ejemplo un cielo totalmente despejado son 0/8, cubierto al 50 % 4/8, y completamente cubierto 8/8.
Asimismo, es conveniente anotar la orientación, tanto en altura como en acimut, de las nubes y su tipología.

Imagen del Sol en la primera fase parcial, se pueden apreciar ligeras trazas nubosas
(Aniceto Porcel - SAG/TOTAL'99)
La nubosidad el 11 de agosto de 1.999 fue un factor que corrió a nuestro favor en las localizaciones escogidas por el equipo TOTAL '99. Al igual que los demás elementos climáticos comentados, la mañana comenzó con índices nubosos con picos relativamente elevados y cambiantes. El mayor valor se obtiene a las 9:06 UT con un 75% cubierto, pero de forma muy puntual. En general, la nubosidad media, previa al eclipse, ronda el 50%. Un valor "alto" pero no demasiado preocupante por su distribución baja en el horizonte. La inestabilidad nubosa continuó un poco más allá de la mitad de la primera parcialidad, con picos que en ningún caso superaron el 40 %. A las 10:36 UT el índice se estabiliza en un 13 % y así se mantuvo hasta los últimos minutos del eclipse, dando un valor del 25 % desde las 12:03 UT hasta las 12:23 UT, periodo en el que están comprendidos los últimos contactos del disco lunar con el solar.

Como se ha mencionado, la distribución general de la nubosidad fue baja en el horizonte. Este factor era especialmente favorable para la observación del eclipse, pues en todo momento el Sol quedó por encima de las brumas y la baja nubosidad. En el emplazamiento dedicado al registro fotográfico y de vídeo solo se notó el paso de nubes sobre el astro solar de forma leve en una fase muy temprana del eclipse, circunstancia que coincide con los picos de las 9:56 UT y las 10:16 UT.
CÁLCULO DE LA DENSIDAD DEL AIRE
Este parámetro se obtiene a partir de la presión atmosférica y la temperatura, siendo directamente proporcional a la primera e indirectamente proporcional a la segunda, y se calcula según la relación aportada por GÜNTER DE ROTH (1979) en su obra "Meteorología":

En la gráfica podemos ver cómo este factor aumenta a lo largo de la mañana en sincronía con el eclipse, volviendo a caer a la salida de este. Su comportamiento es muy lineal, con pequeñas fluctuaciones, a partir de las 10:06 UT, y alcanza su máximo a las 10:59 con 1,171 Kg./m3, 10 minutos después del comienzo de la totalidad. Este pico se mantiene durante 2 minutos, comenzando a descender alrededor de las 11:01 UT. Después de la totalidad se alcanzan valores inferiores a los que se dieron previamente a la misma, llegando a 1,142 Kg./ m3 a las 12:23 UT.

Es obvio que este índice va a mostrar una evolución dependiente de la temperatura y la presión, pues de ellos se deduce. Sin embargo, es interesante comprobar cómo muestra un comportamiento más dominado por la inercia.
INERCIA ATMOSFÉRICA
Comprender los mecanismos que rigen la evolución de un sistema tan complejo y extenso como la atmósfera terrestre es muy difícil. Y es esta característica la que dificulta el poder conocer de forma exhaustiva su evolución y, en consecuencia, cualquier tipo de predicción respecto de su comportamiento futuro. Este campo ha de ser abordado aplicando los conocimientos que tenemos de la mecánica de fluidos, mediante la cual podemos caracterizar, de forma genérica, relaciones causa-efecto a gran escala tanto a nivel cuantitativo como temporal.
En este caso, estamos ante un fenómeno de alcance local con unas características ciertamente únicas respecto de otros sucesos atmosféricos: un eclipse total de sol. Este fenómeno produce una drástica reducción del flujo de radiación solar en un intervalo temporal muy pequeño, volviendo a recuperar unos valores normales de forma análoga. Siempre se ha descrito a los eclipses totales como una noche breve, sin embargo, existen claras diferencias entre el ciclo día-noche y la oscuridad producida al ser ocultado el disco solar por el lunar.
Sabemos que las masas de aire poseen cierta inercia a la hora de reaccionar ante las diversas variables que afectan a su comportamiento, es decir, se manifiestan con cierto retardo temporal respecto a los factores que las provocan. Por otro lado, esta inercia se manifiesta de forma diferenciada para los distintos elementos que caracterizan un comportamiento climatológico. Su efecto no va a ser acusado de la misma forma por la temperatura, la presión atmosférica, la humedad relativa, etc.
El siguiente gráfico modeliza de forma teórica y a título de ejemplo un comportamiento inercial (no siendo representativo de ningún elemento climatológico específico).

Los puntos 1 y 5 corresponden a instantes fuera del eclipse. En cambio, los marcados como 2, 3 y 4 representan el inicio (2), el centro (3) y el fin de la totalidad (4) del eclipse. A su vez los puntos A, B y C representan momentos en los que el elemento climatológico acusa un cambio drástico en su evolución temporal. Como se ve estos están desplazados respecto a los instantes 2, 3 y 4. Si no existiera un comportamiento inercial cabría esperar que coincidieran en el tiempo.
El efecto combinado de la inercia atmosférica y la brevedad temporal del suceso, sobre todo en la fase total, nos va a caracterizar las curvas de evolución de cada elemento, tanto de forma individual como en la relación entre ellos. Obviamente esto ha de tenerse en cuenta a la hora de caracterizar los efectos inducidos por el eclipse en el microclima afectado.
ANÁLISIS ESTADÍSTICO
Por lo visto hasta ahora, se hace evidente que el eclipse total de sol ejerce una clara influencia en la mayoría de los elementos que identifican la climatología local. El siguiente paso es caracterizar su magnitud y su forma. Habiendo observado un alto grado de correlación lineal en las variaciones de algunas magnitudes, hemos decidido realizar un análisis de regresión lineal en las mismas. En esta línea de análisis, los gráficos que vienen a continuación nos ilustran al respecto.
Para el análisis se han utilizado sólo los periodos de tiempo en los que se muestra una tendencia más lineal, es decir, sin una excesiva dispersión y próximos al momento de la totalidad. La escala de tiempo es relativa y esta dividida en dos fases. La primera (AT) se corresponde con el tramo Anterior a la Totalidad que va desde las 10:06 UT (minuto 0) hasta las 10:50 UT (minuto 44) que es el centro de la fase total. La segunda (DT) corresponde al tramo situado Después de la Totalidad, y va desde las 10:50 UT (minuto 0) hasta el final del eclipse a las 12:03 UT (minuto 83). La mayor longitud de esta última fase es posible gracias a una mejora de la estabilidad atmosférica, ya que la primera está influida por la inestabilidad de las primeras horas de la mañana, la nubosidad y la tormenta que se produjo hacia las 3:00 UT.
Temperatura
Tanto al sol como a la sombra la distribución de la temperatura muestra un comportamiento muy homogéneo entre si. El comportamiento inercial es patente, mostrándose muy evidente sobre todo con posterioridad a la totalidad, con un estancamiento en los 20ºC que es la mínima alcanzada en ambas temperaturas.
Temperatura a la sombra

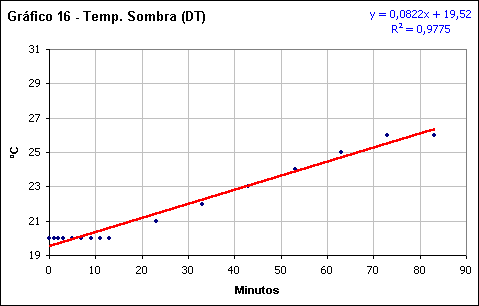
En la fase AT se aprecia como los valores medidos están muy próximos a la línea de tendencia con un coeficiente de regresión lineal de 0,9285, es decir, se ajustan bien a la extrapolación teórica. La pendiente es claramente descendente hacia la totalidad con un valor de -0,0801 ºC/min. Un comportamiento similar se detecta posteriormente a la totalidad (DT) con un coeficiente de regresión lineal aún mas ajustado a la línea de tendencia, con un valor de 0,9775. La pendiente, positiva en este caso, es ligeramente superior al descenso con un valor de 0,0822 ºC/min.
Temperatura al Sol


Tanto la fase AT como la DT muestran altos coeficientes de regresión lineal, con valores de 0,9735 y 0,9726 respectivamente. La pendiente es ligeramente superior durante la bajada hacia la totalidad (AT), aunque muy próxima al valor de la subida tras el eclipse, lo cual indica una clara simetría en la evolución de la temperatura al sol. Respecto de la temperatura a la sombra el ritmo de bajada e incremento medio es de algo más de medio grado por minuto.
Presión atmosférica
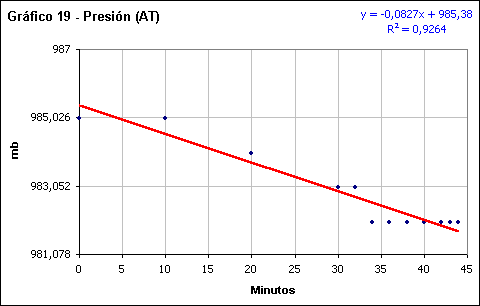
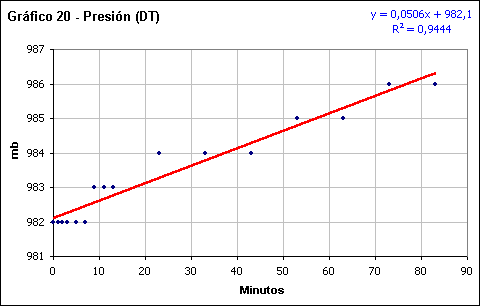
La presión atmosférica muestra un buen ajuste para las fases AT y DT respecto de la línea de tendencia con un coeficiente de regresión lineal por encima de 0,92. Si observamos detenidamente los gráficos vemos como los valores próximos al centro de la totalidad, anterior y posterior a esta, muestran una distribución inercial en los 982 mb.
La pendiente, sin embargo, es claramente diferente, con un descenso de - 0,0827 mb/minuto antes de la fase total del eclipse, frente a 0,0506 mb/minuto después de la totalidad. Esto provoca una ligera asimetría en la evolución temporal de la presión.
Humedad relativa
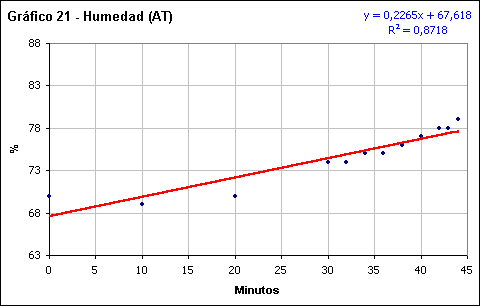
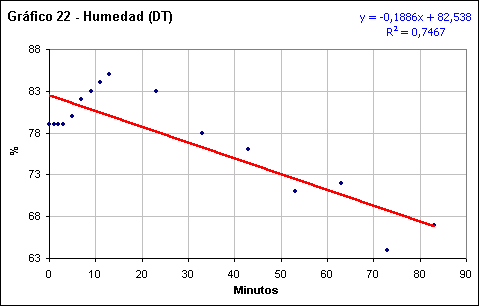
Los valores medidos para este elemento muestran una amplia dispersión, sobre todo tras la totalidad. En este sentido los coeficientes de regresión lineal muestran un ajuste de 0,8718 para la subida hacia el máximo del eclipse y de 0,7467 para la salida de este hasta el final del eclipse. Es llamativa la alta dispersión tras la totalidad, con un incremento rápido de un 6% que se culmina unos 13 minutos después del centro de esta. Es interesante constatar que este comportamiento inercial no se corresponde con otros parámetros, a los que obviamente la humedad relativa está ligada.
El ritmo de incremento medio de la humedad relativa es de un 0,2265% por minuto hasta el centro del eclipse, con una ligera reducción de la pendiente posteriormente, con un valor de -0,1886% por minuto.
Densidad del aire
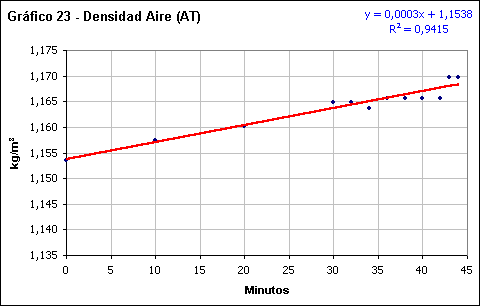
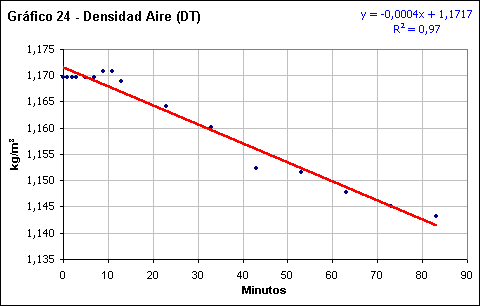
De forma general, muestra una reducida dispersión con un buen ajuste a la línea de tendencia con valores por encima de 0,9. La pendiente es muy suave, con un valor de 0,0003 Kg./m3 durante su ascenso hacia la totalidad, y de -0,0004 Kg./m3 tras esta.
Se puede ver como, tras la fase total, la densidad del aire sufre un ligero aumento que tiene alguna sincronía con el incremento de la humedad relativa, aunque de menor magnitud y ligeramente adelantado temporalmente.
Luminosidad - temperatura

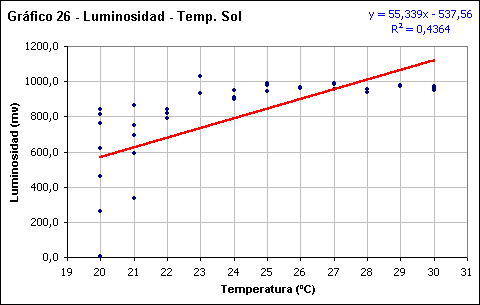
Los gráficos de luminosidad-temperatura no muestran un buen ajuste respecto de la línea de tendencia. La explicación de esto es obvia: estamos enfrentando un elemento que tiene un comportamiento inercial (la temperatura), con un parámetro carente de este (la luminosidad). Como se puede observar, amplios rangos de luminosidad ambiental se corresponden con valores de temperatura sin cambios. La distribución de esto es coherente, pues son los rangos de luminosidad inferior los que más claramente muestran este comportamiento. Esto se debe a que los mínimos valores de luminosidad ambiental se dan en el máximo del eclipse, que es donde, a su vez, se dan los comportamientos inerciales mas acusados. De este modo tenemos que para el mínimo de temperatura de 20ºC a la sombra, se corresponden valores de luminosidad ambiental que van desde 3,20 mv a 866 mv, situación que es prácticamente idéntica para la temperatura al sol. Esta inercia se extiende mas allá del mínimo de temperatura, con una clara disminución conforme aumenta esta.
CONCLUSIONES
Un análisis conjunto de las gráficas muestra evoluciones que podríamos denominar "homogéneas". La temperatura, la presión, la velocidad del viento, y en menor medida, el índice de nubosidad se corresponden con un comportamiento climático, que en líneas generales, se caracteriza por cierta variabilidad en las primeras horas de la mañana y un descenso más o menos pronunciado hasta un mínimo que se alarga significativamente hasta después de la totalidad, con una recuperación hacia los valores habituales al final o después del eclipse. La evolución de la humedad relativa es similar pero lógicamente inversa. En todos los casos, excepto en el índice de nubosidad, la relación causa efecto inducida por el eclipse parece clara. Cabe argumentar, que dada la interdependencia de los diferentes elementos, es difícil que la nubosidad quede al margen de sus influencias, pero esto puede ser matizado, ya que si bien, no podemos describir un comportamiento climático prescindiendo de su relación, hemos de tener en cuenta que el tiempo de respuesta es diferente en cada caso. La importancia de esto, en un suceso tan breve como un eclipse total de sol, estriba en que probablemente la respuesta de algunos parámetros requiera mayor tiempo para mostrar, de forma explícita, su evolución.
Si comparamos el gráfico 14 con la evolución media de los valores obtenidos durante el eclipse comprobamos que existen evidentes diferencias. Según su comportamiento, los elementos pueden ser agrupados en dos categorías:
-
Grupo TPVD (Temperatura, Presión, Velocidad del viento y Densidad del aire): se caracteriza por mostrar una clara evolución dependiente del eclipse, con evidente sincronía temporal con este. Dentro del grupo TPVD comprobamos como sus integrantes muestran un comportamiento inercial al comienzo de la totalidad. Aunque en el caso de la presión y la velocidad del viento se alcanzan los valores mínimos algunos minutos antes del comienzo de esta. Esto puede ser una indicación de que los últimos instantes de la primera parcialidad, donde el residuo de luz solar es muy bajo, pueden tener prácticamente la misma influencia en las masas de aire que en la fase total. Ha esto hemos de sumar el factor de la sensibilidad y tiempo de respuesta instrumental. Como resultado, con los datos que tenemos, no es descartable el efecto inercial en la presión y la velocidad del viento antes de la totalidad, aunque de existir, este queda enmascarado hasta el punto de no ser perceptible en nuestros gráficos.
Respecto de la salida, el grupo TPVD, si que muestra el efecto de la inercia atmosférica. Aunque si asumimos que los valores de luminosidad ambiente minutos antes de la totalidad son tan mínimos, que a efectos de comportamiento atmosférico se solapan con la fase total, esto debe ser aplicable a los minutos posteriores a esta, es decir, debemos asumir un prolongamiento de las valores correspondientes a la totalidad hacia el comienzo de la segunda parcialidad. No obstante la inercia temporal detectada en esta categoría es muy prolongada por lo que cabe asumir un comportamiento de esta naturaleza diferenciado de un umbral mínimo de luminosidad ambiente.
-
Grupo HN (Humedad y Nubosidad): aquí la sincronía temporal en más difusa, y sus gráficas no muestran una clara relación con los puntos de cambio de la pendiente. El grupo NH contiene los parámetros atmosféricos con un comportamiento más difuso respecto de la evolución temporal del eclipse. En el caso de la humedad relativa tenemos un ascenso de los valores hacia un máximo pero desplazado más allá de la totalidad unos 12 minutos, y esto es así por la inercia, aunque en una magnitud inferior a la de otros elementos. Para la nubosidad cualquier interpretación a este respecto casi no tiene sentido, pues si exceptuamos los ligeros incrementos de nubes al comienzo del eclipse, la tónica fue un bajo porcentaje mantenido durante toda la mañana, con lo que incluso la relación causa efecto con el eclipse, de existir, no es demostrable.
Algunas pruebas que hemos realizado durante atardeceres y ocasos solares, muestran algún paralelismo en la evolución de los elementos y parámetros climatológicos observados en el eclipse, pero existen ciertas diferencias. Hemos de tener en cuenta que durante una puesta, el momento de ocultación solar y la bajada de la luz ambiente son fases claramente separadas temporalmente y con una evolución mucho más lenta. En cambio durante un eclipse total de sol, la ocultación completa del disco solar y el descenso de la luz ambiente se aglutinan en un corto espacio de tiempo. En consecuencia, la evolución temporal y los efectos inerciales de la atmósfera se muestran de forma diferente.
Se puede concluir que un eclipse total de sol altera los microclimas situados bajo la sombra de este, en una magnitud notable y de una forma diferenciada de otros sucesos que implican la ausencia de Sol y la disminución de la radiación procedente de este.
Para finalizar, y a modo de ayuda para posteriores investigaciones respecto al tema, sugerimos un análisis previo y posterior de la climatología local de la zona mediante la recogida de datos, para poder detectar aquellas variaciones de magnitudes que no dependan directamente del fenómeno. Una mayor precisión del instrumental y la utilización de un radiómetro puede ayudar a una interpretación más concreta de los fenómenos inerciales observados durante la realización de la experiencia. No obstante, esperamos que este estudio sirva como punto de partida para investigaciones más exhaustivas del fenómeno en futuros eclipses totales de sol.
ANEXO : Altura del sol sobre el horizonte
La altura del Sol sobre el horizonte también es un elemento a tener en cuenta a la hora de hacer un seguimiento de la evolución de los parámetros climatológicos a lo largo del día. En la localización del equipo TOTAL ´99 la máxima altura de nuestro astro prácticamente coincide con la totalidad. Esto es un indicativo de que nos hallábamos próximos a la zona del máximo del eclipse, es decir la ciudad de Rimnicu-Vilcea en Rumania. La siguiente gráfica muestra la altura del sol sobre el horizonte en función del tiempo en la zona de Balatonlelle durante la mañana del 11 de agosto de 1.999.

BIBLIOGRAFÍA
BARRY, R.G. y CHORLEY, R.J., Atmósfera, tiempo y clima, Barcelona, Omega, 1971.
BATTAN, L. J., El tiempo atmosférico, Barcelona, Omega, 1976.
BIELZA DE ORY, V., Geografía general, Madrid, Taurus, 1989.
CUADRAT, J. Mª y PITA, Mª F., Climatología, Madrid, Cátedra, 2000.
D. ROTH, G., Meteorología, Barcelona, Omega, 1979.
MARTÍN VIDE, J. y OLCINA CAMPOS, J., Tiempos y climas mundiales, Barcelona, Oikos-tau, 1996.
MARTÍN VIDE, J., Fundamentos de climatología analítica, Barcelona, Síntesis, 1991.
MEDINA, M., Iniciación a la Meteorología, Barcelona, Salvat, 1986.
MILLER, A., Meteorología, Barcelona, Labor, 1972.
PEIXOTO, J. y OORT, A., Physics of climate, New York, American Institute of Physics, 1992.
WEB DE INTERÉS
-
Web de Observatorio Arval (Paraguaná) del eclipse total de sol del 26 de febrero de 1998.
-
Medición cambios atmosféricos locales durante un eclipse solar
AGRADECIMIENTOS Y COLABORACIONES
-
José Luís Ortiz, investigador del Grupo de Atmósferas Planetarias del Instituto de Astrofísica de Andalucía (IAA) del Consejo Superior de Investigaciones Científicas (CSIC).
-
Al personal del Servicio Meteorológico de Aeropuerto de Granada.
-
Departamento de Climatología de la Facultad de Ciencias de la Universidad de Granada.
-
Al resto de los miembros del equipo TOTAL '99: Alberto López, Antonio Gálvez, Antonio Molina, J. Manuel Barruezo, Javier Pérez, Jesús Cano, Jesús Ríos, Loly Martín, Loren Madrid, Mª José Caballero.


